My research is focused on the development of predictive multiscale models of complex biomaterials and biological processes involved in the initiation, growth, and metastases of tumors. Such advances involve several formidable challenges at the interface of modern computational engineering and biological science including (1) Development of multiscale mathematical models of cancer evolution, (2) Employment of experimental data to inform computational models, while coping with uncertainties in the models and measurements, and (3) Assessment of uncertainty in the computational prediction and patient specific decision making. My current research aims to address some of these grand-challenge areas through development and computational implementation of mathematical models of cancer evolution in subcell-cellular-tissue scales as well as statistical and computational data-driven algorithms to integrate imaging data and models.
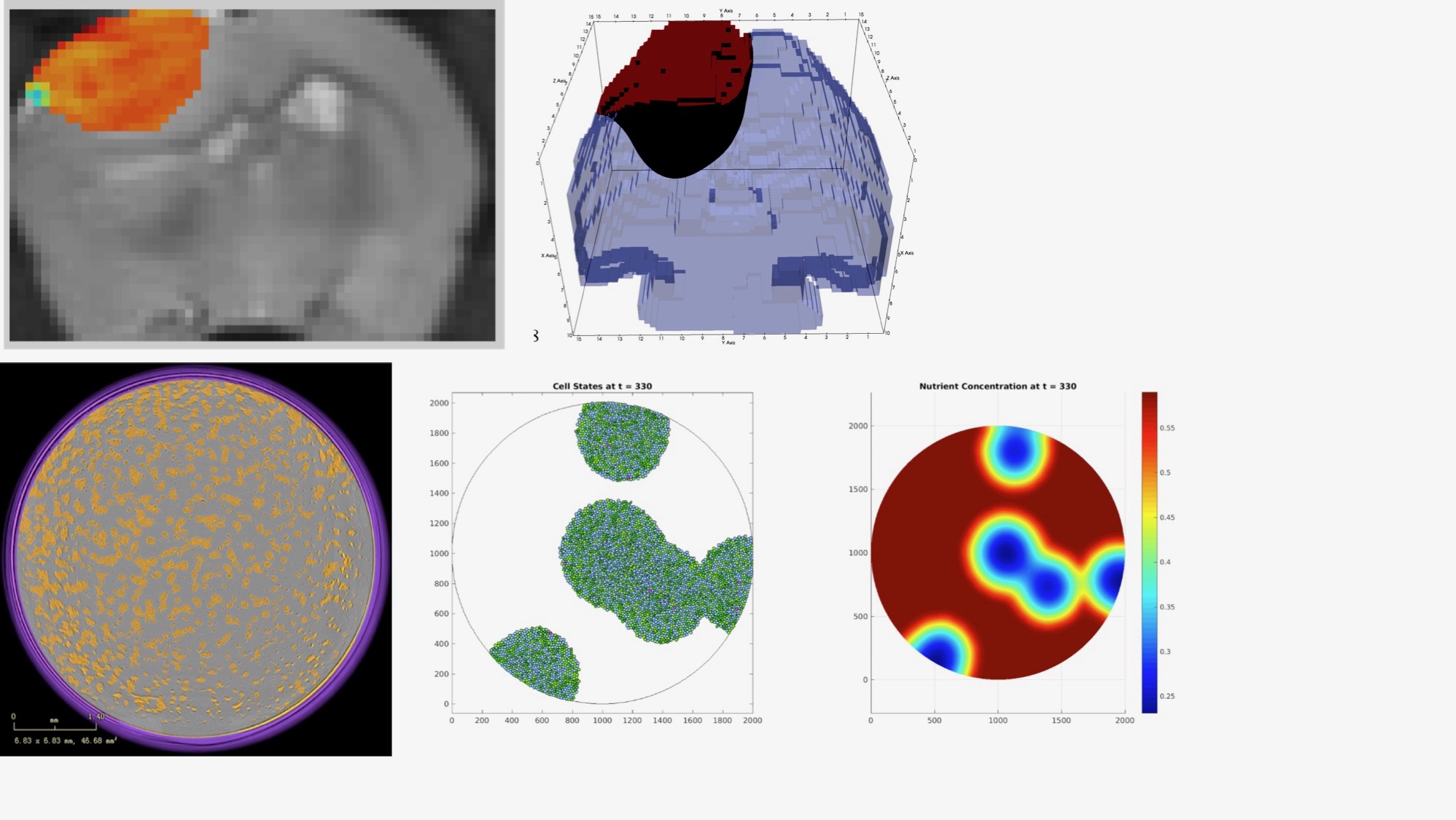
Multiscale Models of Cancer Growth Of particular interest is simulating the effects of mechanical deformation on tissue growth through development of fully coupled mass transport (phase-field) and finite strain deformation (hyperelastic) theories derived from principles of continuum mixture theory. Furthermore, I work on reduced order hybrid multiscale models consists of continuum model of the dispersion of nutrients and growth factors in the tumor microenvironment (tissue scale), lattice-free agent-based model to describe individual cell dynamics including cell movement and the phenotypic transitions (cellular scale), and inter- and intracellular signaling pathways models represented by a system of coupled nonlinear differential equations (sub-cellular scale).
Computational Frameworks for Data-enabled Predictive Modeling My work also involves development and implementation of advanced statistical and computational methods to inform the parameters of the multiscale models using relevant in vivo and in vitro experimental data, systematically quantify the uncertainties in model parameters, and assess the reliability of computational predictions. The data-enabled frameworks are developed based on Bayesian approach for bringing together model-specific experimental data for model calibration and validation.